CALCULATING CATHODE FOLLOWER INPUT RESISTANCE
Richard Matthews
Leeds Radio
Brooklyn NY
718 963-1764
The treatment given assumes the following:
a) the input signal does not drive the grid too close to 0 volts (ie no
grid current)
b) the circuit is operating below, say 40 khz.
Input and output signals in cathode follower are in phase. To see this, imagine what would happen if you were to apply a positive going pulse between grid and ground; the plate current would increase. When the plate current increases, the voltage across Rk also increases (with the side of Rk connected to the cathode becoming more positive with respect to ground). Think of the voltage between the grid and cathode terminals as vin'. It is clear that vin' + vrk1 +vrk2 = vin (by kirchoffs voltage law) You may now think of a cathode follower as a amplifier that uses 100 percent of its output voltage as series-negative feedback.
(1) Cathode Follower Gain = µ(Rk)/(Rp+(µ)(Rk))
The above equation is true when circuit is not externally loaded. For gain with external load substitute Rk| |RL (Where RL is the external load.)
It can be seen that
(2) limRk->inf µ(Rk)/(Rp+(µ)(Rk)) = 1
and so an assumption that we will use later is sound, and not a "rule of thumb".
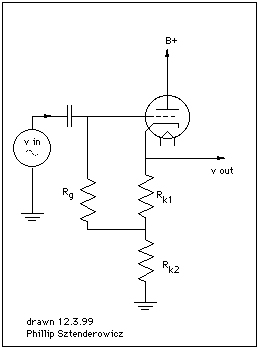
For component identification, please refer to diagram at the bottom of page.
We will define:
vin = the amplifier input voltage
Av = voltage gain
Rin = small signal input resistance
iin= input current
(3) iin = (vin - vx)/Rg
(4) Rin = vin/iin = vin/(vin-vx)/Rg = vinRg/(vin-vx)
(5) vx = vin*Av*(Rk2/(Rk1+Rk2))
From (2) we know that Av is approximetely equal to 1.
So:
(6) Rin = vinRg/ (vin-vin(Rk2/ (Rk1+Rk2))
factoring out vin
(7) Rin= Rg/(1-Rk2/(Rk1+Rk2))
Note how when Rk2= 0, that Rin = Rg
